• Overview
• Example: Simple Arithmetic Expressions
• Formal Definition
• Example: Boolean Expressions, Assignment Statements, and If Statements
• Self-Study #1
• The Language Defined by a CFG
• Leftmost and Rightmost Derivations
• Parse Trees
• Self-Study #2

Recall that the input to the parser is a sequence of tokens (received interactively, via calls to the scanner). The parser:

• Groups the tokens into "grammatical phrases".
• Discovers the underlying structure of the program.
• Finds syntax errors.
• Perhaps also performs some actions to find other kinds of errors.

The output depends on whether the input is a syntactically legal program; if so, then the output is some representation of the program:

• an abstract-syntax tree (maybe + a symbol table),
• or intermediate code,
• or object code.

We know that we can use regular expressions to define languages (for example, the languages of the tokens to be recognized by the scanner). Can we use them to define the language to be recognized by the parser? Unfortunately, the answer is no. Regular expressions are not powerful enough to define many aspects of a programming language's syntax. For example, a regular expression cannot be used to specify that the parentheses in an expression must be balanced, or that every ``else'' statement has a corresponding ``if''. Furthermore, a regular expression doesn't say anything about underlying structure. For example, the following regular expression defines integer arithmetic involving addition, subtraction, multiplication, and division:

digit+ (("+" | "-" | "*" | "/") digit+)*

Example: Simple Arithmetic ExpressionsL

We can write a context-free grammar (CFG) for the language of (very simple) arithmetic expressions involving only subtraction and division. In English:

• An integer is an arithmetic expression.
• If exp₁ and exp₂ are arithmetic expressions, then so are the following:
  • exp₁ - exp₂
  • exp₁ / exp₂
  • ( exp₁ )

And here is how to understand the grammar:

• The grammar has five terminal symbols: intliteral minus divide lparen rparen. The terminals of a grammar used to define a programming language are the tokens returned by the scanner.
• The grammar has one nonterminal: Exp (note that a single name, Exp, is used instead of Exp₁ and Exp₂ as in the English definition above).
• The grammar has four productions or rules, each of the form:
  Exp $\longrightarrow$ ...
  A production left-hand side is a single nonterminal. A production right-hand side is either the special symbol $\varepsilon$ (the same $\varepsilon$ that can be used in a regular expression) or a sequence of one or more terminals and/or nonterminals (there is no rule with $\varepsilon$ on the right-hand side in the example given above).

A more compact way to write this grammar is:

Intuitively, the vertical bar means "or", but do not be fooled into thinking that the right-hand sides of grammar rules can contain regular expression operators! This use of the vertical bar is just shorthand for writing multiple rules with the same left-hand-side nonterminal.

A CFG is a 4-tuple $\left( N, \Sigma, P, S \right)$ where:

• $N$ is a set of nonterminals.
• $\Sigma$ is a set of terminals.
• $P$ is a set of productions (or rules).
• $S$ is the start nonterminal (sometimes called the goal nonterminal) in $N$. If not specified, then it is the nonterminal that appears on the left-hand side of the first production.

Example: Boolean Expressions, Assignment Statements, and If StatementsL

The language of boolean expressions can be defined in English as follows:

• "true" is a boolean expression, recognized by the token true.
• "false" is a boolean expression, recognized by the token false.
• If exp₁ and exp₂ are boolean expressions, then so are the following:
  • exp₁ || exp₂
  • exp₁ && exp₂
  • ! exp₁
  • ( exp₁ )

Here is a CFG for a language of very simple assignment statements (only statements that assign a boolean value to an identifier):

Stmt $\;\longrightarrow\;$ id  assign  BExp  semicolon

We can "combine" the two grammars given above, and add two more rules to get a grammar that defines a language of (very simple) if-statements. In words, an if-statement is:

1. The word "if", followed by a boolean expression in parentheses, followed by a statement, or
2. The word "if", followed by a boolean expression in parentheses, followed by a statement, followed by the word "else", followed by a statement.

Here is the combined context-free grammar:

The language defined by a context-free grammar is the set of strings (sequences of terminals) that can be derived from the start nonterminal. What does it mean to derive something?

• Start by setting the "current sequence" to be the start nonterminal.
• Repeat:
  • find a nonterminal $X$ in the current sequence;
  • find a production in the grammar with $X$ on the left (i.e., of the form $X$ → $\alpha$, where $\alpha$ is either $\varepsilon$ (the empty string) or a sequence of terminals and/or nonterminals);
  • Create a new "current sequence" in which $\alpha$ replaces the $X$ found above;
  until the current sequence contains no nonterminals.

Thus, we arrive either at $\varepsilon$ or at a string of terminals. That is how we derive a string in the language defined by a CFG.

Below is an example derivation, using the 4 productions for the grammar of arithmetic expressions given above. In this derivation, we use the actual lexemes instead of the token names (e.g., we use the symbol "-" instead of minus).

Exp $\Longrightarrow$ Exp - Exp$\Longrightarrow$ 1 - Exp$\Longrightarrow$ 1 - Exp / Exp$\Longrightarrow$ 1 - Exp / 2 $\Longrightarrow$ 1 - 4 / 2

And here is some useful notation:

• $\Longrightarrow$ means derives in one step
• $\stackrel{+}\Longrightarrow$ means derives in one or more steps
• $\stackrel{*}\Longrightarrow$ means derives in zero or more steps

So, given the above example, we could write: Exp $\stackrel{+}\Longrightarrow$ 1 - Exp / Exp.

A more formal definition of what it means for a CFG $G$ to define a language may be stated as follows:

Leftmost and Rightmost DerivationsL

There are several kinds of derivations that are important. A derivation is a leftmost derivation if it is always the leftmost nonterminal that is chosen to be replaced. It is a rightmost derivation if it is always the rightmost one.

Parse TreesL

Another way to derive things using a context-free grammar is to construct a parse tree (also called a derivation tree) as follows:

• Start with the start nonterminal.
• Repeat:
  • choose a leaf nonterminal $X$
  • choose a production $X \longrightarrow \alpha$
  • the symbols in $\alpha$ become the children of $X$ in the tree
  until there are no more leaf nonterminals left.

The derived string is formed by reading the leaf nodes from left to right.

Here is the example expression grammar given above:

Exp $\longrightarrow$ intliteral  | Exp minus Exp  | Exp divide Exp  | lparen Exp rparen

and, using that grammar, here's a parse tree for the string 1 - 4 / 2:

---

Self-Study #2L Below is the CFG for very simple if-statements used earlier.

Stmt $\;\longrightarrow\;$ if lparen BExp rparen Stmt
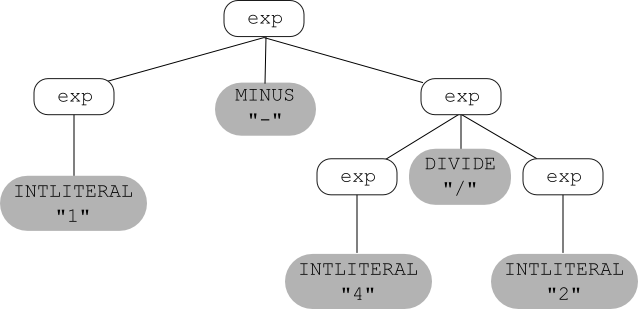
Stmt $\;\longrightarrow\;$ if lparen BExp rparen Stmt else Stmt
Stmt $\;\longrightarrow\;$ id assign BExp semicolon
BExp $\;\longrightarrow\;$ true
BExp $\;\longrightarrow\;$ false
BExp $\;\longrightarrow\;$ BExp or BExp
BExp $\;\longrightarrow\;$ BExp and BExp
BExp $\;\longrightarrow\;$ not BExp
BExp $\;\longrightarrow\;$ lparen BExp rparen

Question 1: Give a derivation for the string: if (! true ) x = false; Is your derivation leftmost, rightmost, or neither?

Question 2: Give a parse tree for the same string.

solution