• Overview
• Ambiguous Grammars
• Disambiguating Grammars
• Precedence
• Associativity
• Test Yourself #1
• Resolving Ambiguity
• Test Yourself #2
• List Grammars
• A Grammar for a Programming Language
• Summary

The following grammar (recalled from the prior) defines a simple language of mathematical expressions (with the productions numbered for reference):

Consider the string

which would be tokenized as

It should be readily apparent to you that the string is recognized by the the language, and can be produced via the (leftmost) derivation sequence:

This derivation sequence corresponds to the parse tree:

However, inspection of the grammar also reveals that there is another leftmost derivation that can recognize the string by choosing to apply the rules differently:

Step #1. Exp $\Longrightarrow$ Exp divide Exp (via production P₃)
Step #2.    $\;\;\;\;\;\Longrightarrow$ Exp minus Exp divide Exp (via production P₂)
Step #3.    $\;\;\;\;\;\Longrightarrow$ intlit minus Exp divide Exp (via production P₁)
Step #4.    $\;\;\;\;\;\Longrightarrow$ intlit minus intlit divide Exp (via production P₁)
Step #5.    $\;\;\;\;\;\Longrightarrow$ intlit minus intlit divide intlit (via production P₁)

Which corresponds to the parse tree:

If for grammar $G$ and string $w$ there is:

• more than one leftmost derivation of $w$ or,
• more than one rightmost derivation of $w$, or
• more than one parse tree for $w$

then G is called an ambiguous grammar. (Note: the three conditions given above are equivalent; if one is true then all three are true.)

It is worth noting that ambiguity is not a problem for certain applications of Context-Free Grammars. As discussed in the intro, language recognition is satisfied by finding a one derivation for the string, and the string will certainly maintain membership in the language if there is more than one derivation possible. However, for the task of parsing, ambiguous grammars cause problems, both in the correctness of the parse tree and in the efficiency of building it. We will briefly explore both of these issues.

A problem of correctness: The major issue with ambiguous parse trees is that the underlying structure of the language is ill-defined. In the above example, subtraction and division can swap precedence; the first parse tree groups 4/2, while the second groups 1-4. These two groupings correspond to expressions with different values: the first tree corresponds to (1-(4/2)) and the second tree corresponds to ((1-4)/2).

A problem of efficiency: As we will see later, a parser can use significantly more efficient algorithms (in terms of Big-O complexity) by adding constraints to the language that it recognizes. One such assumption of some parsing algorithms is that the language recognized is unambiguous. To some extent, this issue can come up independently of correctness. For example, the following grammar has no issue of grouping (it only ever produces intlit), but production P₁ can be applied any number of times before producing the integer literal token.

It's useful to know how to translate an ambiguous grammar into an equivalent unambiguous grammar Since every programming language includes expressions, we will discuss these operations in the context of an expression language. We are particularly interesting in forcing unambiguous precedence and associativies of the operators.

To write a grammar whose parse trees express precedence correctly, use a different nonterminal for each precedence level. Start by writing a rule for the operator(s) with the lowest precedence ("-" in our case), then write a rule for the operator(s) with the next lowest precedence, etc:

Now let's try using these new rules to build parse trees for

First, a parse tree that correctly reflects that fact that division has higher precedence than subtraction:

Now we'll try to construct a parse tree that shows the wrong precedence:

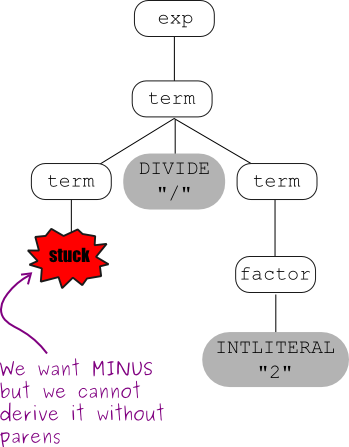
This grammar captures operator precedence, but it is still ambiguous! Parse trees using this grammar may not correctly express the fact that both subtraction and division are left associative; e.g., the expression: 5-3-2 is equivalent to: ((5-3)-2) and not to: (5-(3-2)).

Draw two parse trees for the expression 5-3-2 using the current expression grammar:

exp → exp MINUS exp | term
term → term DIVIDE term | factor
factor → INTLITERAL | LPAREN exp RPAREN

solution

• A grammar is recursive in nonterminal $X$ if: $$X \stackrel{+}\longrightarrow{\Tiny\dots\,}X{\Tiny\,\dots}$$ (in one or more steps, $X$ derives a sequence of symbols that includes an $X$).
• A grammar is left recursive in $X$ if: $$X \stackrel{+}\longrightarrow X{\Tiny\,\dots}$$ (in one or more steps, $X$ derives a sequence of symbols that starts with an $X$).
• A grammar is right recursive in $X$ if: $$X \stackrel{+}\longrightarrow {\Tiny\dots\,}X$$ (in one or more steps, $X$ derives a sequence of symbols that ends with an $X$).

The grammar given above for arithmetic expressions is both left and right recursive in nonterminals Exp and Term (try writing the derivation steps that show this).

To write a grammar that correctly expresses operator associativity:

• For left associativity, use left recursion.
• For right associativity, use right recursion.

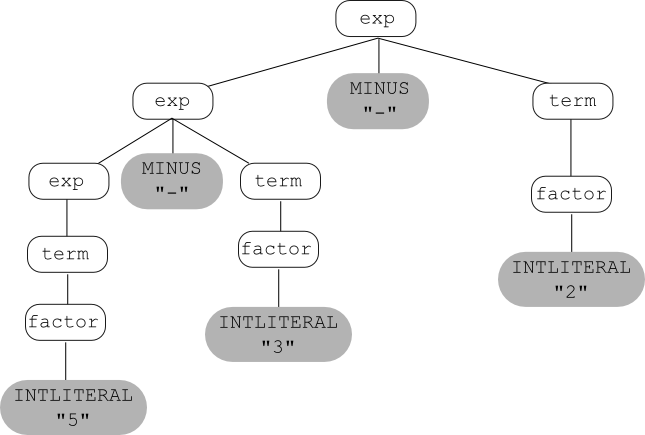
Here's the correct grammar:

And here's the (one and only) parse tree that can be built for 5 - 3 - 2 using this grammar:

Now let's consider a more complete expression grammar, for arithmetic expressions with addition, multiplication, and exponentiation, as well as subtraction and division. We'll use the token pow for the exponentiation operator, and we'll use "**" as the corresponding lexeme; e.g., "two to the third power" would be written: 2 ** 3, and the corresponding sequence of tokens would be: intlit pow intlit.

Here's an ambiguous context-free grammar for this language:

First, we'll modify the grammar so that parse trees correctly reflect the fact that addition and subtraction have the same, lowest precedence; multiplication and division have the same, middle precedence; and exponentiation has the highest precedence:

This grammar is still ambiguous; it does not yet reflect the associativities of the operators. So next we'll modify the grammar so that parse trees correctly reflect the fact that all of the operators except exponentiation are left associative (and exponentiation is right associative; e.g., 2**3**4 is equivalent to: 2**(3**4)):

Finally, we'll modify the grammar by adding a unary operator, unary minus, which has the highest precedence of all (e.g., -3**4 is equivalent to: (-3)**4, not to -(3**4). Note that the notion of associativity does not apply to unary operators, since associativity only comes into play in an expression of the form: x op y op z.

Below is the grammar we used earlier for the language of boolean expressions, with two possible operands: true and false, and three possible operators: and, or, not:

Question 1: Add nonterminals so that or has lowest precedence, then and, then not. Then change the grammar to reflect the fact that both and and or are left associative.

Question 2: Draw a parse tree (using your final grammar for Question 1) for the expression: true and not true.

solution

List Grammars

Another kind of grammar that you will often need to write is a grammar that defines a list of something. There are several common forms. For each form given below, we provide three different grammars that define the specified list language.

• One or more PLUSes (without any separator or terminator). (Remember, any of the following three grammars defines this language; you don't need all three lines).
  1. xList $\longrightarrow$ PLUS | xList xList
  2. xList $\longrightarrow$ PLUS | xList PLUS
  3. xList $\longrightarrow$ PLUS | PLUS xList
• One or more runs of one or more PLUSes, each run separated by commas:
  1. xList $\longrightarrow$ PLUS | xList COMMA xList
  2. xList $\longrightarrow$ PLUS | xList COMMA PLUS
  3. xList $\longrightarrow$ PLUS | PLUS COMMA xList
• One or more PLUSes, each PLUS terminated by a semi-colon:
  1. xList $\longrightarrow$ PLUS SEMICOLON | xList xList
  2. xList $\longrightarrow$ PLUS SEMICOLON | xList PLUS SEMICOLON
  3. xList $\longrightarrow$ PLUS SEMICOLON | PLUS SEMICOLON xList
• Zero or more PLUSes (without any separator or terminator):
  1. xList $\longrightarrow$ $\varepsilon$ | PLUS | xList xList
  2. xList $\longrightarrow$ $\varepsilon$ | PLUS | xList PLUS
  3. xList $\longrightarrow$ $\varepsilon$ | PLUS | PLUS xList
• Zero or more PLUSes, each PLUS terminated by a semi-colon:
  1. xList $\longrightarrow$ $\varepsilon$ | PLUS SEMICOLON | xList xList
  2. xList $\longrightarrow$ $\varepsilon$ | PLUS SEMICOLON | xList PLUS SEMICOLON
  3. xList $\longrightarrow$ $\varepsilon$ | PLUS SEMICOLON | PLUS SEMICOLON xList
• The trickiest kind of list is a list of zero or more x's, separated by commas. To get it right, think of the definition as follows:
  Either an empty list, or a non-empty list of x's separated by commas.
  We already know how to write a grammar for a non-empty list of x's separated by commas, so now it's easy to write the grammar:

  xList	$\longrightarrow$	$\varepsilon$ | nonemptyList
  nonemptyList	$\longrightarrow$	PLUS | PLUS COMMA nonemptyList

A Grammar for a Programming Language

Using CFGs for programming language syntax has the notational advantage that the problem can be broken down into pieces. For example, let us begin sketching out a simple scripting language, that starts with productions for some top-level nonterminals: