---

Contents

• Motivation and Definition
• Example 1: Value of an Arithmetic Expression
• Example 2: Type of an Expression
• Test Yourself #1

Motivation and Definition

The goal of the parser is to produce output that can be consumed by the next phase of the compiler. Thus far, we have considered using a Context-Free Grammar as a convenient mechanism for defining what strings are syntactically valid programs in the language, and we have discussed techniques for altering the Context-Free Grammar such that the parse trees for those strings match the intended structure of the program. In summary, we've explored how to specify parse trees for a given token stream. However, the parse tree is a relatively cumbersome data structure to work with, made worse by the very alterations we introduced to aid in parsing. For our purposes, we will consider the parse tree to be a purely transitional data structure, useful for structuring the token stream, and then consumed to create the final output to be forwarded on to syntactic analysis.

This reading introduces a method for specifying how to derive a result from a parse tree. This specification is known as a syntax-directed definition (SDD), while the entire technique is known as syntax-directed translation (SDT). The general technique of SDT is applicable for a variety of parsing tasks. To introduce SDD, we will explore several examples of mapping parse trees to a variety of different results, but the application we are ultimately interested in for compilers is to translate a parse tree into an AST. In this reading from parse trees abstract-syntax trees, known as a syntax-directed definition. The name is apt, as the key feature of a syntax-directed definition is that it intermingles the definition

This involves doing a syntax-directed translation -- translating from a sequence of tokens to some other form, based on the underlying syntax.

A syntax-directed translation is defined by augmenting the CFG: a translation rule is defined for each production. A translation rule defines the translation of the left-hand side nonterminal as a function of:

• constants
• the right-hand-side nonterminals' translations
• the right-hand-side tokens' values (e.g., the integer value associated with an INTLITERAL token, or the String value associated with an ID token)

To translate an input string:

1. Build the parse tree.
2. Use the translation rules to compute the translation of each nonterminal in the tree, working bottom up (since a nonterminal's value may depend on the value of the symbols on the right-hand side, you need to work bottom-up so that those values are available).

The translation of the string is the translation of the parse tree's root nonterminal.

Example 1L

Below is the definition of a syntax-directed translation that translates an arithmetic expression to its integer value. When a nonterminal occurs more than once in a grammar rule, the corresponding translation rule uses subscripts to identify a particular instance of that nonterminal. For example, the rule

has two Exp nonterminals; Exp₁ means the left-hand-side Exp, and Exp₂ means the right-hand-side Exp.

Also, the notation xxx.value is used to mean the value associated with token xxx and the notation YYY.trans is used to mean the translation associated with nonterminal YYY.

CFG Production				Translation Rule
Exp	$\longrightarrow$	Exp plus Term		Exp1.trans = Exp2.trans $+$ Term.trans
Exp	$\longrightarrow$	Term		Exp.trans = Term.trans
Term	$\longrightarrow$	Term times Factor		Term1.trans = Term2.trans $\times$ Factor.trans
Term	$\longrightarrow$	Factor		Term.trans = Factor.trans
Factor	$\longrightarrow$	intlit		Factor.trans = intlit.value
Factor	$\longrightarrow$	lparens Exp rparens		Factor.trans = Exp.trans

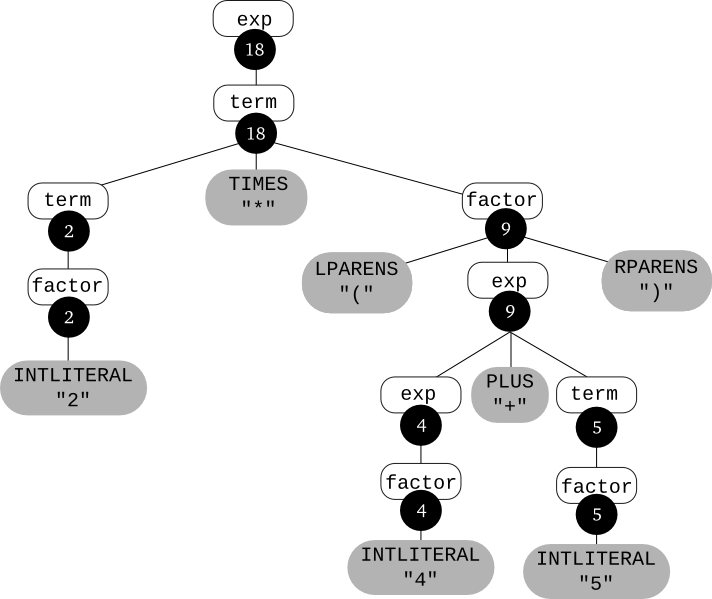
Consider evaluating these rules on the input 2 * (4 + 5). The result is the following annotated parse tree:

Example 2L

Consider a language of expressions that use the three operators: +, &&, == using the terminal symbols plus, and, equals, respectively. Integer literals are represented by the same intlit token we've used before, and true and false represent the literals true and false (note that we could have just as well defined a single boollit token that the scanner would populate with either $true$ or $false$).

Let's define a syntax-directed translation that type checks these expressions; i.e., for type-correct expressions, the translation will be the type of the expression (either $int$ or $bool$), and for expressions that involve type errors, the translation will be the special value $error$. We'll use the following type rules:

1. Both operands of the + operator must be of type $int$.
2. Both operands of the && operator must be of type $bool$.
3. Both operands of the == operator must have the same (non-$error$) type.

Here is the CFG and the translation rules:

CFG Production				Translation Rule
Exp	$\longrightarrow$	Exp  plus  Term		if $($Exp2.trans == $int$$)$ and $($Term.trans == $int$$)$ then       Exp1.trans = $int$ else      Exp1.trans = $error$
Exp	$\longrightarrow$	Exp  and  Term		if $($Exp2.trans == $bool$$)$ and $($Term.trans == $bool$$)$ then       Exp1.trans = $bool$ else      Exp1.trans = $error$
Exp	$\longrightarrow$	Exp  equals  Term		if $($Exp2.trans == Term.trans$)$ and $($Term.trans $\neq$ $error$$)$ then       Exp1.trans = $bool$ else      Exp1.trans = $error$
Exp	$\longrightarrow$	Term		Exp.trans = Term.trans
Term	$\longrightarrow$	true		Term.trans = $bool$
Term	$\longrightarrow$	false		Term.trans = $bool$
Term	$\longrightarrow$	intlit		Term.trans = $int$
Term	$\longrightarrow$	lparens  Exp  rparens		Term.trans = Exp.trans

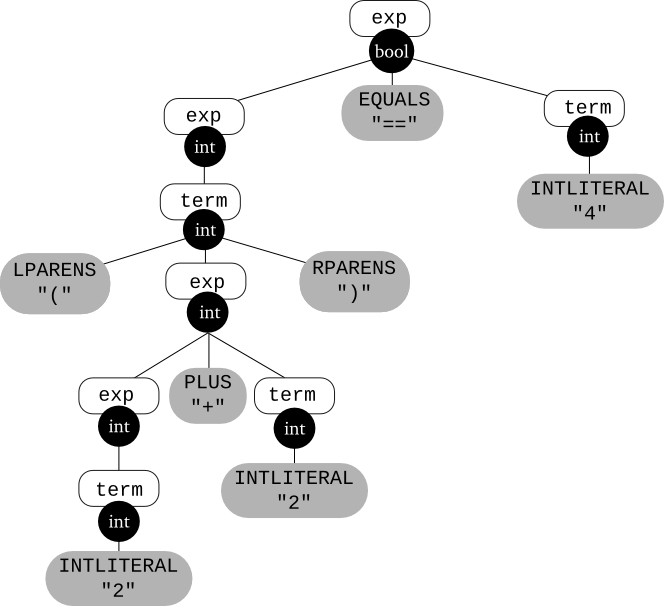
Here's an annotated parse tree for the input (2 + 2) == 4