Contents

• Overview
• Finite-State Machines
  • Example: Pascal Identifiers
  • Self Study #1
  • Example: Integer Literals
  • Formal Definition
  • Deterministic and Non-Deterministic FSMs
  • How to Implement a FSM
• Regular Expressions
  • Self Study #2
  • Example: Integer Literals
  • The Language Defined by a Regular Expression
• Using Regular Expressions and Finite-State Machines to Define a Scanner
  • Self Study #3

OverviewL

Recall that the job of the scanner is to translate the sequence of characters that is the input to the compiler to a corresponding sequence of tokens. In particular, each time the scanner is called it should find the longest sequence of characters in the input, starting with the current character, that corresponds to a token, and should return that token.

It is possible to write a scanner from scratch, but it is often much easier and less error-prone approach is to use a scanner generator like lex or flex (which produce C or C++ code), or jlex (which produces java code). The input to a scanner generator includes one regular expression for each token (and for each construct that must be recognized and ignored, such as whitespace and comments). Therefore, to use a scanner generator you need to understand regular expressions. To understand how the scanner generator produces code that correctly recognizes the strings defined by the regular expressions, you need to understand finite-state machines (FSMs).

Finite State MachinesL

A finite-state machine is similar to a compiler in that:

• A compiler recognizes legal programs in some (source) language.
• A finite-state machine recognizes legal strings in some language.

In both cases, the input (the program or the string) is a sequence of characters.

A FSM is applied to an input (a sequence of characters). It either accepts or rejects that input. Here's how the FSM works:

• The FSM starts in its start state.
• If there is a edge out of the current state whose label matches the current input character, then the FSM moves to the state pointed to by that edge, and "consumes" that character; otherwise, it gets stuck.
• The finite-state machine stops when it gets stuck or when it has consumed all of the input characters.

An input string is accepted by a FSM if:

• The entire string is consumed (the machine did not get stuck), and
• the machine ends in a final state.

The language defined by a FSM is the set of strings accepted by the FSM.

The following strings are in the language of the FSM shown above:

• x
• tmp2
• XyZzy
• position27

The following strings are not in the language of the FSM shown above:

• 123
• a?
• 13apples

Let us consider another example of an FSM:

Example: Integer LiteralsL

Formal Definition

An FSM is a 5-tuple: $(Q,\Sigma,\delta,q,F)$

• $Q$ is a finite set of states ($\{\mathrm{S,A,B}\}$ in the above example).
• $\Sigma$ (an uppercase sigma) is the alphabet of the machine, a finite set of characters that label the edges ($\{+,-,0,1,...,9\}$ in the above example).
• $q$ is the start state, an element of $Q$ ($\mathrm{S}$ in the above example).
• $F$ is the set of final states, a subset of $Q$ ({B} in the above example).
• $\delta$ is the state transition relation: $Q \times \Sigma \rightarrow Q$ (i.e., it is a function that takes two arguments -- a state in $Q$ and a character in $\Sigma$ -- and returns a state in $Q$).

Here's a definition of $\delta$ for the above example, using a state transition table:

Deterministic and Non-Deterministic FSMsL

There are two kinds of FSM:

1. Deterministic:
   • No state has more than one outgoing edge with the same label.
2. Non-Deterministic:
   • States may have more than one outgoing edge with same label.
   • Edges may be labeled with $\varepsilon$ (epsilon), the empty string. The FSM can take an $\varepsilon$-transition without looking at the current input character.

Example

Here is a non-deterministic finite-state machine that recognizes the same language as the second example deterministic FSM above (the language of integer literals with an optional sign):

Sometimes, non-deterministic machines are simpler than deterministic ones, though not in this example.

A string is accepted by a non-deterministic finite-state machine if there exists a sequence of moves starting in the start state, ending in a final state, that consumes the entire string. For example, here's what happens when the above machine is run on the input "+75":

After scanning		Can be in these states
(nothing)		$S$	$A$
$+$		$A$	(stuck)
$+7$		$B$	(stuck)
$+75$		$B$	(stuck)

There is one sequence of moves that consumes the entire input and ends in a final state (state B), so this input is accepted by his machine.

It is worth noting that there is a theorem that says:

For every non-deterministic finite-state machine $M$, there exists a deterministic machine $M'$ such that $M$ and $M'$ accept the same language.

How to Implement a FSM

The most straightforward way to program a (deterministic) finite-state machine is to use a table-driven approach. This approach uses a table with one row for each state in the machine, and one column for each possible character. Table[j][k] tells which state to go to from state j on character k. (An empty entry corresponds to the machine getting stuck, which means that the input should be rejected.)

Recall the table for the (deterministic) "integer literal" FSM given above:

The table-driven program for a FSM works as follows:

• Have a variable named state, initialized to S (the start state).
• Repeat:
  • read the next character from the input
  • use the table to assign a new value to the state variable
  until the machine gets stuck (the table entry is empty) or the entire input is read. If the machine gets stuck, reject the input. Otherwise, if the current state is a final state, accept the input; otherwise, reject it.

Regular Expressions

Regular expressions provide a compact way to define a language that can be accepted by a finite-state machine. Regular expressions are used in the input to a scanner generator to define each token, and to define things like whitespace and comments that do not correspond to tokens, but must be recognized and ignored.

As an example, recall that a Pascal identifier consists of a letter, followed by zero or more letters or digits. The regular expression for the language of Pascal identifiers is:

letter . (letter | digit)*

The following table explains the symbols used in this regular expression:

Often, the "followed by" dot is omitted, and just writing two things next to each other means that one follows the other. For example:

letter (letter | digit)*

In fact, the operands of a regular expression should be single characters or the special character epsilon, meaning the empty string (just as the labels on the edges of a FSM should be single characters or epsilon). In the above example, "letter" is used as a shorthand for:

a | b | c | ... | z | A | ... | Z

and similarly for "digit". Also, we sometimes put the characters in quotes (this is necessary if you want to use a vertical bar, a dot, or a star character).

To understand a regular expression, it is necessary to know the precedences of the three operators. They can be understood by analogy with the arithmetic operators for addition, multiplication, and exponentiation:

Regular Expression Operator	Analogous Arithmetic Operator	Precedence
|	plus	lowest precedence
.	times	middle
*	exponentiation	highest precedence

So, for example, the regular expression:

$\mathrm{letter}.\mathrm{letter} | \mathrm{digit}\mathrm{^*}$

does not define the same language as the expression given above. Since the dot operator has higher precedence than the | operator (and the * operator has the highest precedence of all), this expression is the same as:

$(\mathrm{letter}.\mathrm{letter}) | (\mathrm{digit}\mathrm{^*})$

and it means "either two letters, or zero or more digits".

Example: Integer LiteralsL

Let's re-examine the example of integer literals for regular-expressions:

The Language Defined by a Regular ExpressionL

Every regular expression defines a language: the set of strings that match the expression. We will not give a formal definition here, instead, we'll give some examples:

Regular Expression		Corresponding Set of Strings
$\varepsilon$		$\{$""$\}$
a		$\{$"a"$\}$
a.b.c		$\{$"abc"$\}$
a | b | c		$\{$"a", "b", "c"$\}$
(a | b | c)*		$\{$"", "a", "b", "c", "aa", "ab",  $\ldots$,  "bccabb", $\ldots$ $\}$

Using Regular Expressions and FSMs to Define a ScannerL

There is a theorem that says that for every regular expression, there is a finite-state machine that defines the same language, and vice versa. This is relevant to scanning because it is usually easy to define the tokens of a language using regular expressions, and then those regular expression can be converted to finite-state machines (which can actually be programmed).

For example, let's consider a very simple language: the language of assignment statements in which the left-hand side is a Pascal identifier (a letter followed by one or more letters or digits), and the right-hand side is one of the following:

• ID + ID
• ID * ID
• ID == ID

This language has five tokens, which can be defined by the following five regular expressions:

Token	Regular Expression
assign	"="
id	letter (letter | digit)*
plus	"$+$"
times	"$*$"
equals	"="."="

These regular expressions can be converted into the following finite-state machines:

assign:
id:
plus:
times:
equals:

Given a FSM for each token, how do we write a scanner? Recall that the goal of a scanner is to find the longest prefix of the current input that corresponds to a token. This has two consequences:

1. The scanner sometimes needs to look one or more characters beyond the last character of the current token, and then needs to "put back" those characters so that the next time the scanner is called it will have the correct current character. For example, when scanning a program written in the simple assignment-statement language defined above, if the input is "==", the scanner should return the EQUALS token, not two ASSIGN tokens. So if the current character is "=", the scanner must look at the next character to see whether it is another "=" (in which case it will return EQUALS), or is some other character (in which case it will put that character back and return ASSIGN).

2. It is no longer correct to run the FSM program until the machine gets stuck or end-of-input is reached, since in general the input will correspond to many tokens, not just a single token.

Furthermore, remember that regular expressions are used both to define tokens and to define things that must be recognized and skipped (like whitespace and comments). In the first case a value (the current token) must be returned when the regular expression is matched, but in the second case the scanner should simply start up again trying to match another regular expression.

With all this in mind, to create a scanner from a set of FSMs, we must:

• modify the machines so that a state can have an associated action to "put back N characters" and/or to "return token XXX",
• we must combine the finite-state machines for all of the tokens in to a single machine, and
• we must write a program for the "combined" machine.

For example, the FSM that recognizes Pascal identifiers must be modified as follows:

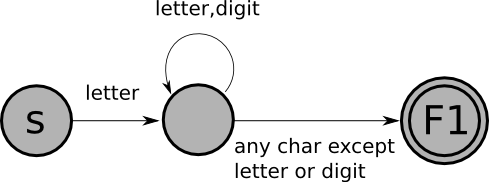
with the following table of actions:

And here is the combined FSM for the five tokens (with the actions noted below):

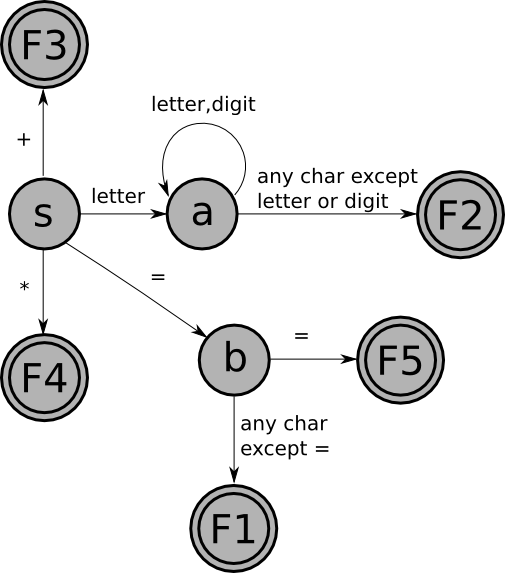
with the following table of actions:

We can convert this FSM to code using the table-driven technique described above, with a few small modifications:

• The table will include a column for end-of-file as well as for all possible characters (the end-of-file column is needed, for example, so that the scanner works correctly when an identifier is the last token in the input).
• Each table entry may include an action as well as or instead of a new state.
• Instead of repeating "read a character; update the state variable" until the machine gets stuck or the entire input is read, the code will repeat: "read a character; perform the action and/or update the state variable" (eventually, the action will be to return a value, so the scanner code will stop, and will start again in the start state next time it is called).

Here's the table for the above "combined" FSM:

	+	*	=	$\mathrm{letter}$	$\mathrm{digit}$	EOF
$S$	return plus	return times	$B$	$A$
$A$	put back 1 char; return id	put back 1 char; return id	put back 1 char; return id	$A$	$A$	return id
$B$	put back 1 char; return assign	put back 1 char; return assign	return equals	put back 1 char; return assign	put back 1 char; return assign	return assign