EECS665 – Compiler Construction

Abstract-Syntax Trees

ContentsL

Topic Introduction
The AST vs the Parse Tree
ASTs for Program Constructs
Translation Rules That Build an AST
Test Yourself #2

(Part of Syntactic-Analysis)

Topic IntroductionL

While Syntax-Directed Definition serves as a general technique for specifying translations of trees for many purposes, one particular application of SDD is of special interest to compiler writers: inducing an Abstract-Syntax Tree (AST) from the Parse Tree. The AST can be thought of as a condensed form of the parse tree, elliding incidental syntactic details of the program input.

Students occasionally are surprised that the conceptual workflow of the compiler is to build the parse tree only to immediately discard it in favor of a different tree data structure. In this chapter we will discuss what the AST is, how the AST differs from the parse tree, and how an SDD may be specified to produce an AST from a parse tree. Hopefully, this treatment communicates why the parse tree is a useful part of syntactic analysis, as well as why the AST is a superior internal representation for later phases of the compiler. It's also worth mentioning that in practice, the parse tree and AST are constructed at the same time in a memory-efficient way that keeps much of the parse tree implicit.

The AST vs the Parse TreeL

First, let's identify the ways in which an abstract-syntax tree (AST) differs from a parse tree:

Operators appear at internal nodes instead of at leaves.
"Chains" of single productions are collapsed.
Lists are "flattened".
Syntactic details (e.g., parentheses, commas, semi-colons) are omitted.

In general, the AST is a better structure for later stages of the compiler because it omits details having to do with the source language, and just contains information about the essential structure of the program.

Below is an example of the parse tree and the AST for the expression 3 * (4 + 2) using the usual arithmetic-expression grammar that reflects the precedences and associativities of the operators. Note that the parentheses are not needed in the AST because the structure of the AST defines how the subexpressions are grouped.

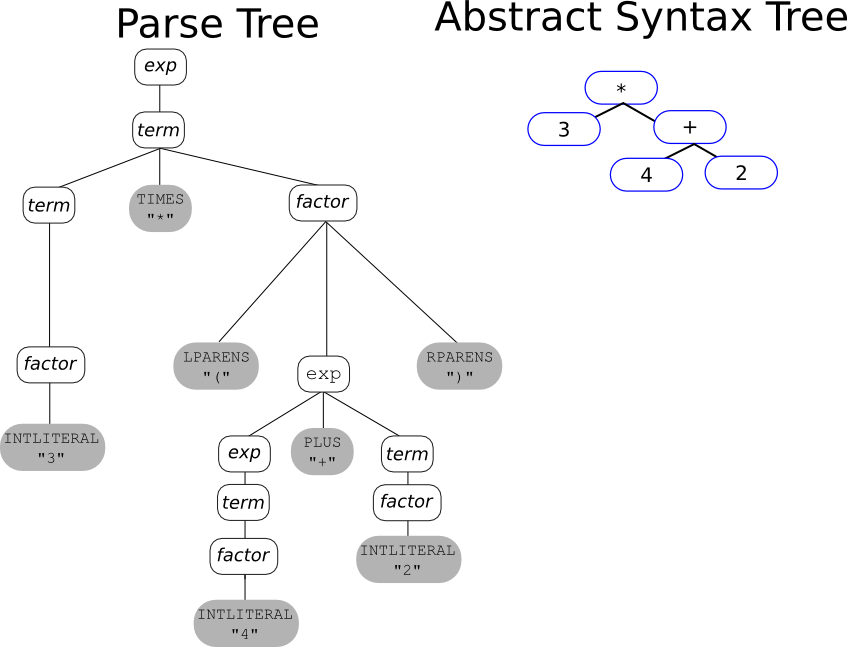
It's worth noting a couple of relationships between AST and parse tree:

The grouping symbols are necessary to build the particular parse tree in this example (since otherwise the higher-precedence of multiplication would have grouped the 3 with the 4), and the grouping symbols must be kept as leaves of the parse tree in order to fulfill the property that reading the frontier of the parse tree yields the complete token stream. However, the grouping is implicit in the AST via the parent-child relationship of AST nodes.
Because the abstract syntax tree omits syntactic details, many parse trees may yield the same abstract syntax tree. For example, the following input strings would have different parse trees but the same AST as the one above:
- (3 * (4 + 2))
- (3) * ((4) + (2))
- 3 * ((4 + 2))
- (3 * (4 + 2))

The many-to-one nature of parse trees to ASTs is a feature, and it is indicative of the AST as being a more condensed representation of the program. It also indicates that some Parse Tree could be ``unparsed'' from an AST, but it might not be the original parse tree.

ASTs for Program ConstructsL

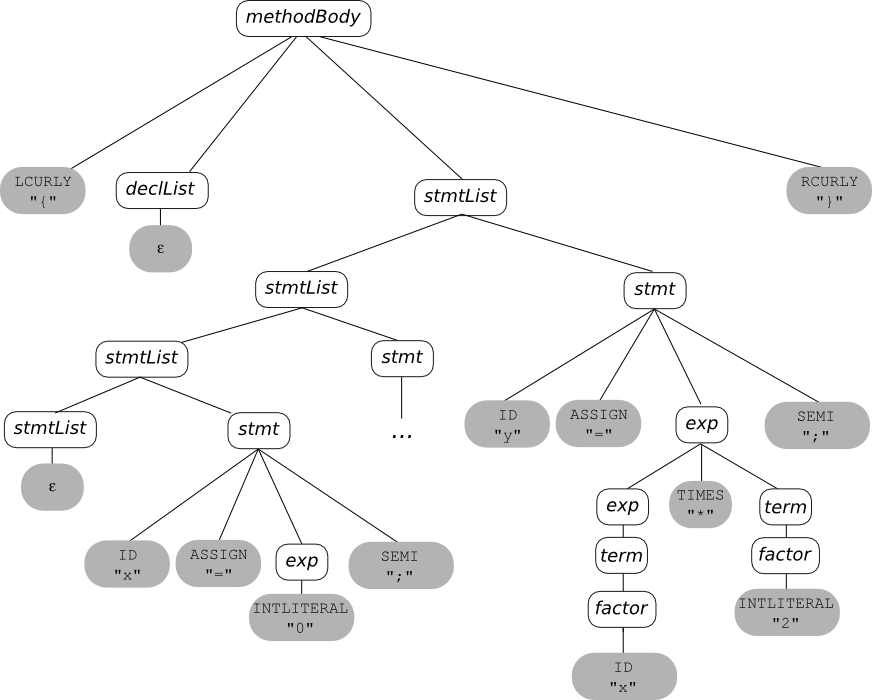
For constructs other than expressions, the compiler writer has some choices when defining the AST -- but remember that lists (e.g., lists of declarations lists of statements, lists of parameters) should be flattened, that operators (e.g., "assign", "while", "if") go at internal nodes, not at leaves, and that syntactic details are omitted.

Input
=====

{               
   x = 0;        
   while (x<10) { 
      x = x+1;     
   }      
   y = x*2;
}

Note that in the AST there is just one stmtList node, with a list of three children (the list of statements has been "flattened"). Also, the "operators" for the statements (assign and while) have been "moved up" to internal nodes (instead of appearing as tokens at the leaves). And finally, syntactic details (curly braces and semi-colons) have been omitted.

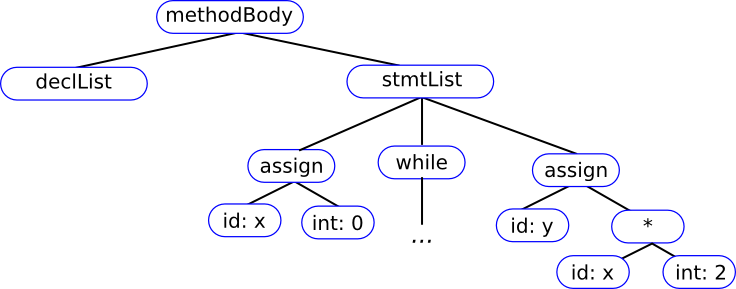
Translation Rules That Build an ASTL

To define a syntax-directed translation so that the translation of an input is the corresponding AST, we first need operations that create AST nodes. Let's use some object-oriented pseudocode, and assume that we have the following class hierarchy:

class ExpNode { }

class IntLitNode extends ExpNode {
    public IntLitNode(int val) {...}
}

class PlusNode extends ExpNode {
    public PlusNode( ExpNode e1, ExpNode e2 ) { ... }
}

class TimesNode extends ExpNode {
    public TimesNode( ExpNode e1, ExpNode e2 ) { ... }
}

Now we can define a syntax-directed translation for simple arithmetic expressions, so that the translation of an expression is its AST:

CFG Production Translation rules

exp $\longrightarrow$ exp PLUS term exp₁.trans = new PlusNode(exp₂, term.trans)

exp $\longrightarrow$ term exp.trans = term.trans

term $\longrightarrow$ term TIMES factor term₁.trans = new TimesNode(term₂.trans, factor.trans)

term $\longrightarrow$ factor term.trans = factor.trans

factor $\longrightarrow$ INTLITERAL factor.trans = new IntLitNode(INTLITERAL.value)

factor $\longrightarrow$ LPARENS exp RPARENS factor.trans = exp.trans

Self-StudyL

Illustrate the syntax-directed translation defined above by drawing the parse tree for the expression 2 + 3 * 4, and annotating the parse tree with its translation (i.e., each nonterminal in the tree will have a pointer to the AST node that is the root of the subtree of the AST that is the nonterminal's translation).

solution

CFG Production			Translation rules
exp	$\longrightarrow$	exp `PLUS` term	exp₁.trans = new PlusNode(exp₂, term.trans)
exp	$\longrightarrow$	term	exp.trans = term.trans
term	$\longrightarrow$	term `TIMES` factor	term₁.trans = new TimesNode(term₂.trans, factor.trans)
term	$\longrightarrow$	factor	term.trans = factor.trans
factor	$\longrightarrow$	`INTLITERAL`	factor.trans = new IntLitNode(`INTLITERAL`.value)
factor	$\longrightarrow$	`LPARENS` exp `RPARENS`	factor.trans = exp.trans